Present value of an annuity (PVOA)

This article explains the computation of present value of an annuity (PVOA). If you want to learn the computation of present value of a single sum to be received or paid in future, read “present value of a single payment in future” article.

What is present value (PV)?

Let’s first understand the concept of present value and then proceed to what is an annuity and how its present value is computed.

In accounting, finance and capital budgeting, the term present value means today’s value of a sum of money to be received at a point of time in future. It is based on the concept of time value of money, which states that the money available today is more valuable than the same amount of money available in future. By this concept, a one time payment of $1,000 received today is worth more than the same amount spread over ten annual payments of $100 each. The reason is that the person who owns $1,000 today has an opportunity to invest it somewhere and generate more cash over ten-year period.

Now, lets suppose, you have $5,000 in hand today and you find an opportunity to invest this money at 10% annual interest rate. If invested, your money will grow to $5,500 in one year, as computed below:

= $5,000 + ($5,000 x 10%)
= $5,000 + ($5,000 x 0.1)
= $5,000 + $500
= $5,500

It means that $5,000 today is worth $5,500 in one-year period, if invested at 10% interest rate. Therefore, the present value of your money is $5,000 and its future value is $5,500.

Let’s take it the other way. The sum of $5,500 to be received after one year is a future value cash flow. Yet, its value today would be its present value, which again would be $5,000 assuming a discount rate of 10%.

What is an annuity?

Before talking about the present value of an annuity, lets understand the meanings and concept of annuity. Annuity means a stream or series of equal cash payments. Suppose, for example, you have made an investment that will generate an interest income of $5,000 for you at the end of each year for five years. The income of $5,000 that you will receive at the end of each year is an annuity for you. Thus, an annuity can be defined as a stream of regular cash payments to an individual person (or another entity) over a certain period of time.

Annuities can be divided into two types – immediate annuities and deferred annuities. Immediate annuities, as the name implies, are those annuities that start paying immediately. Deferred annuities, as the name implies, are those annuities that start paying after a certain predefined period of delay.

What is present value of an annuity (PVOA)?

The present value of an annuity (PVOA) refers to today’s value of all the payments that an annuity is expected to generate over its whole life. To obtain the PVOA, we must discount the whole series of payments back to its present value using a given discount rate.

The present value of an annuity is largely affected by the discount rate used to bring future payments to their present value. The lower the discount rate, the higher the present value, and vice versa.

Other factors that affect an annuity’s current worth include the number of payments, the amount of payments and the timing of cash flows. It is, therefore, much important to know about these factors before concluding your financial decisions about an annuity.

If you are considering to sell your annuity as an option to meet your immediate cash needs, then understanding the present value of an annuity is much important to you. It helps you compare the total amount of all the payments of your annuity over time to its equivalent current worth and decide whether you should keep or sell your annuity [Source: annuity.org].

Formula and calculation of present value of an annuity (PVOA)

A commonly used formula for discounting an annuity to its present value is given below:

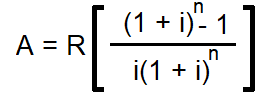
Where;

• A = Present value of an annuity
• R = Amount of an annuity
• i = Discount rate (Interest rate or rate of return)
• n = Number of periods

Examples of PVOA

Let’s exemplify the computation of present value of an annuity to further elaborate the concept.

Example 1

Southern Company has made an investment in government bonds. The bonds will generate an interest income of $25,000 each year for the company for a five-year period. The interest rate is 10% compounded annually.

Required: Compute present value of this stream of interest income.

Solution

A = R[{(1 + i)ⁿ – 1}/{i(1 + i)ⁿ}]
= $25,000 × [{(1 + 0.1)⁵ – 1}/{0.1(1 + 0.1)⁵}]
= $25,000 × [{(1.1)⁵ – 1}/{0.1(1.1)⁵}]
= $25,000 × [{1.61051 – 1}/{0.1(1.61051)}]
= $25,000 × [0.61051/0.161051]
= $25,000 × 3.791
= $94,775

At 10% interest rate compounded annually, the present value of this annuity is $94,775.

The use of present value of an annuity of $1 in arrears table:

The computations involved in above solution might be complex and time consuming, especially for those with weak mathematical skills. Luckily, we can reduce our computational burden by taking the value of [{(1 + i)ⁿ – 1}/{i(1 + i)ⁿ}] from present value of an annuity of $1 in arrears table. This table provides the present value of $1 to be received (or paid) each year over a series of years at various interest rates.

Let’s use the table and see how much computational work it eliminates for us.

A = R[{(1 + i)ⁿ – 1}/{i(1 + i)ⁿ}]
= $25,000 × [{(1 + 0.1)⁵ – 1}/{0.1(1 + 0.1)⁵}]
= $25,000 × 3.791*
= $94,775

*Value of [{(1 + 0.1)⁵ – 1}/{0.1(1 + 0.1)⁵}] from present value of an annuity of $1 in arrears table:
10% interest rate, 5 periods.

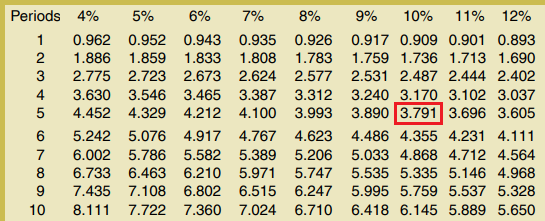
Notice that we have still used the same formula as in the first solution. However, incorporating the use of table in the solution has reduced our computational work to great extent. In this solution, we have just multiplied the annual payment by the discount factor 3.791 directly taken from the table. This factor is the value of expression “[{(1 + 0.1)⁵ – 1}/{0.1(1 + 0.1)⁵}]”, and is known as present value interest factor of annuity (PVIFA). You can see this factor in above table where 5-period row and 10% column intersect each other.

When PVIFA is directly obtained from the table, a more appropriate way of presenting formula and solution is as follows:

A = R(PVIFA_{i%, n})
= $25,000(PVIFA_{10%, 5})
= $25,000 × 3.791
= $94,775

The PVOA concept explained so far has been summarized below:

Example 2

Western Company expects a series of 24 monthly receipts of $3,600 each. The first payment will be received 1 month from today. Determine the present value of this series of payments assuming an interest rate of 12% per year compounded semi-annually.

Solution

The question states that the interest is compounded semi-annually (i.e., twice a year). So, the annual interest rate of 12% must be divided by 2 to obtain the value of “i” as follows:
i = 12%/2 = 6%

A = R(PVIFA_{i%, n})
= $3,600(PVIFA_{6%, 24})
= $3,600 × 12.550*
= $45,180

*Value from present value of an annuity of $1 in arrears table:
6% interest rate, 24 periods.

Present value of an annuity concept in capital budgeting

Capital investments often require an initial investment and then generate a series of cash flows – much similar to annuities. Therefore, to know the true profitability of a project, managers must know the concept of annuities and their present value.

Net present value (NPV), internal rate of return (IRR), profitability index (PI) and discounted payback period (DPP) method are the most commonly used tools for making capital budgeting decisions. All these methodologies incorporate the concept of present value in generating their output to be used by managers and decision makers.

Example 3

The management of Graham Inc. has identified an investment opportunity requiring an initial cash outlay of $80,000. The expected cash inflow from this investment is $20,000 per year for 8 years.

Required:

1. Calculate the present value of all cash inflows from this investment opportunity assuming a discount rate of 12%.
2. Calculate the net present value of this opportunity.
3. Give your opinion regarding acceptance or rejection of this opportunity.

Solution

(1). Present value of all cash inflows:

Notice that this investment opportunity works like an annuity, as it promises to generate 8 consecutive annual cash inflows of $20,000 each. Therefore, the present value of this whole series of cash inflows can be obtained by applying the present value of an annuity formula as follows:

A = R(PVIFA_{i%, n})
= $20,000 × (PVIFA_{12%, 8})
= 20,000 × 4.968*
= $99,360

*Value from present value of an annuity of $1 in arrears table:
12% interest rate, 8 periods.

(2). Net present value (NPV) of the opportunity:

The net present value (NPV) of an investment opportunity can be obtained by deducting the present value (PV) of initial investment from the present value (PV) of cash inflows.

NPV = PV of cash inflows – PV of initial investment
= $99,360 – $80,000
= $19,360

(3). Opinion regarding acceptance or rejection:

According to net present value analysis, the investment in this opportunity is acceptable because it promises a positive NPV of $19,360. A positive NPV number means the NPV of all cash inflows is greater than the NPV of all cash outflows, and the investment is profitable.

Practice exercises and problems
Practice quizzes