Present value of a single payment in future

The value of money changes over time. The value of a dollar in hand today is more than the value of a dollar to be received a year from now, because if you have a dollar in hand today, you can invest it in a security and earn some interest on it. This concept is known as time value of money.

The present value of an amount refers to today’s value of the amount to be received at a point of time in future. The concept of present value is frequently used in capital budgeting techniques and its understanding is important for managers, business owners and others involved in making capital budgeting decisions. Examples of capital budgeting techniques that take into account the present value of money are net present value (NPV) method, internal rate of return (IRR) method and discounted payback method.

The present value is computed either for a single payment or a series of payments to be received in future. This article explains the computation of present value of a single payment to be received at a single point of time in future. To understand the computation of present value of a series of payments to be received in future, read present value of an annuity article.

Present value of a single payment formula:

The formula to calculate present value of a single sum is give below:

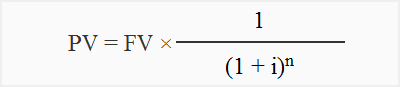
Where;

• PV = Present value of the amount
• FV = Future value of the amount to be received in future
• i = Interest rate in percentage
• n = Number of periods after which the amount will be received in future

The following examples explain the computation of present value of a single payment.

Example 1:

A company is expecting to receive $5,000 four years from now. Compute present value of this sum if the current market interest rate is 10% and the interest is compounded annually.

Solution:

To find the present value, the amount of $5,000 to be received in future would be discounted using the given interest rate of 10%.

Number of periods (n) = 4 and Interest rate (i) = 10% or 0.1

By putting the values of ‘n’ and ‘i’ into present value of a single sum formula:

PV = FV × [1/(1 + i)ⁿ]
= $5,000 × [1/(1 + 10%)⁴]
= $5,000 × [1/(1 + 0.1)⁴]
= $5,000 × [1/(1.1)⁴]
= $5,000 × [1/1.4641]
=$5,000 × 0.683
= $3,415

The amount of $5,000 to be received after four years has a present value of $3,415. It means if the amount of $3,415 is invested today @10% per year compounded annually, it will grow to $5,000 in 4 years.

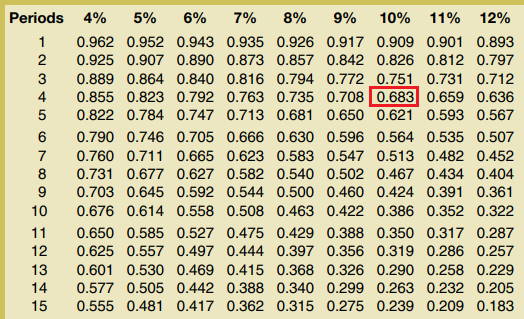
Alternatively, we can simplify our computational work by obtaining the value of expression [1/(1 + i)ⁿ] directly from present value of $1 table. This value is known as present value interest factor (PVIF) of $1.

The present value of $1 table contains the present value of $1 to be received (or paid) after different periods at various interest rates. Let’s use the table and see how it simplies our computations.

Use of present value of $1 table:

Number of periods (n) = 4 and Interest rate (i) = 10% or 0.1

PV = FV × [1/(1 + i)ⁿ]
= $5,000 × [1/(1 + 10%)⁴]
=$5,000 × 0.683*
= $3,415

*Value of [1/(1 + 10%)⁴] from present value of $1 table:
10% interest rate, 4th period

When present value interest factor (PVIF) is directly taken from the table, a better way to present the formula and solution is as follows:

PV = FV × PVIF_{i%, n}
= $5,000 × PVIF_{10%, 4}
= $5,000 × 0.683*
= $3,415

*Value from present value of $1 table:
10% interest rate, 4th period

Let’s use the table again in example 2 below.

Example 2:

A company wants to accumulate $600,000 in 5 years. The interest rate is 12% compounded semi-annually.

Required:

1. What amount should be invested today?
2. How much interest will be earned in five years?

Solution:

(1) Amount to be invested today:

The interest is compounded semi-annually therefore the number of years would be multiplied by 2 to obtain ‘n’ and the interest rate would be divided by 2 to obtain ‘i’:

n = 5 × 2 = 10
i = 12%/2 = 6% or 0.06

PV = FV × PVIF_{i%, n}
= FV × PVIF_{6%, 10}
= $600,000 × 0.558*
= $334,800

*Value from present value of $1 table:
6% interest rate, 10th period

(2) The amount of interest that will be earned over 5-year period:

= $600,000 – $334,800
= $265,200

At 12% interest per year compounded semi-annually, the company needs to invest $334,000 today to accumulate $600,000 in 5 years. The total interest income of $265,200 will be earned over the period.

Practice exercises and problems
Practice quizzes