Simple and compound interest

Interest may be defined as the charge for using the borrowed money. It is an expense for the person who borrows money and income for the person who lends money. Interest is charged on principal amount at a certain rate for a certain period. For example, 10% per year, 4% per quarter or 2% per month etc.  Principal amount means the amount of money that is originally borrowed from an individual or a financial institution. It does not include interest. In practice, the interest is charged using one of two methods. These are:

1. simple interest method; and
2. compound interest method

These two methods are briefly explained below:

Simple interest method:

Under this method, the interest is charged only on the amount originally lent (principal amount) to the borrower. Interest is not charged on any accumulated interest under this method. Simple interest is usually charged on short-term borrowings.

Simple interest formula:

Simple interest can be easily computed using the following formula:

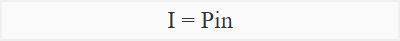
Where;

• I = Simple interest in dollars
• P = Principal amount
• i = Rate of interest
• n = Number of periods

Example 1:

A loan of $10,000 has been issued for 6-years. Compute the amount to be repaid by borrower to the lender if simple interest is charged @ 5% per year.

Solution:

P = $1,000; i = 5%; n = 5

By putting the values of P, i and n into the simple interest formula:

I = P × i × n
= $10,000 × 5% × 6
= $10,000 × .05 × 6
= $3,000

At the end of sixth year, the amount of $13,000 (i.e., $10,000 principal + $3,000 interest for six years) will be repaid to the lender.

Compound interest method:

Compounding of interest is very common. Under this method, the interest is charged on principal plus any accumulated interest. The amount of interest for a period is added to the amount of principal to compute the interest for next period. In other words, the interest is reinvested to earn more interest. The interest may be compounded monthly, quarterly, semi-annually or annually depending on the terms and conditions of loan agreement. Consider the following example to understand how compounding of interest works.

Example 2:

Suppose, you have deposited $100 with a bank for five years at a rate of 5% per year compounded annually. The interest for the first year will be computed on $100 and you will have $105 ($100 principal + $5 interest) at the end of first year. The interest for the second year will be computed on $105 and at the end of second year you will have $110.25 ($105 principal + 5.25 interest). The interest for the third year will be computed on $110.25 and at the end of third year you will have $115.76 (110.25 principal + 5.51 interest). The following table shows the computation for 5-year period of investment.

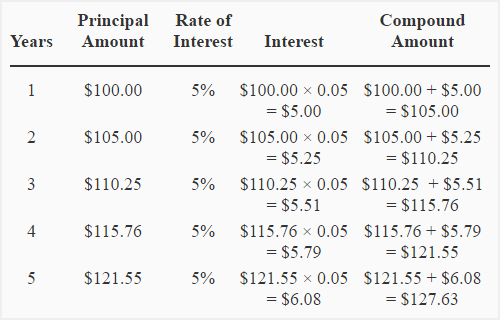
Under compound interest system, when interest is added to the principal amount, the resulting amount is known as compound amount. In the above table, the compound amount at the end of each year have been computed in the last column. Notice that the compound amount at the end of an year becomes the principal amount to compute the interest for the next year.

Compound amount and compound interest formula:

The above procedure of computing compound amount and compound interest is lengthy and time consuming. Fortunately, the formulas are available to compute compound amount and compound interest for any number of periods.

(i). Compound amount formula:

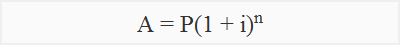
Where;

• A = Compound amount
• P = Principal amount
• i = rate of interest
• n = number of periods

(ii). Compound interest formula:

Compound interest = Compound amount – Principal amount

Example 3:

The City Bank has issued a loan of $100 to a sole proprietor for a period of 5-years. The interest rate for this loan is 5% and the interest is to be compounded annually. Compute

1. compound amount
2. compound interest

1. Computation of compound amount:

A = P(1 + i)ⁿ
= $1,000 × (1 + 5%)⁵
= $1,000 × (1 + .05)⁵
= $1,000 × (1.05)⁵
= $1,000 × 1.276
= $1,276

2. Computation of compound interest:

Once the compound amount has been computed, the amount of interest earned over the investment period can be computed by subtracting principal amount from the compound amount. In this example, the principle amount is $1,000 and the compound amount computed above is $1,276. The amount of compound interest for the fiver year period can be computed as follows:

Compound interest = Compound amount – Principle amount
= $1276 – $1,000
= $276

Use of future value of $1 table to compute compound amount:

The shortest and easiest method to compute compound amount is to use the future value of $1 table. This table contains the value of (1 + i)ⁿ for a given value of i and n. After locating the value of  (1 + i)ⁿ in the table, the principal amount is simply multiplied with the value to find the compound amount. The principal amount is then subtracted from compound amount to get the amount of compound interest for the given interest rate and time period.

= $1,000 × (1 + 5%)⁵
= $1,000 × 1.276*
= $1,276

Compound interest : $1,276 – $1,000 = $276

*Value of (1 + 5%)⁵ from future value of $1 table: 5 periods; 5% interest rate.

The future value tables are widely used in accounting and finance to save time and avoid unnecessary computations.

Compound interest is always greater than simple interest:

Compound interest is always greater than simple interest and the reason is very simple. Under simple interest system, the interest is computed only on principal amount whereas under compound interest system, the interest is computed on principle as well as on any interest accumulated up to the date of calculation. Consider the following example for the explanation of this point:

Example 4:

A woman has deposited $6,000 in a saving bank which pays here interest at a rate of 9% per year.

Required: Compute the amount of interest that will be earned over 12-year period:

1. if the interest is simple?
2. if the interest is compounded annually?

Solution:

(1) Simple interest:

= $6,000 × 0.09 × 12
= $6,480

(2) Compound interest:

= $6,000 × (1 + 9%)¹²
= $6,000 × 2.813*
= $16,878

Compound interest = $16,878 – $6,000
= $10,878

Notice that compound interest is more than simple interest by $4,398 ($10,878 – $6,480).

*Value of (1 + 9%)¹² from future value of $1 table: 12 periods; 9% interest rate.

Try our simple interest calculator and compound interest calculator

Practice exercises and problems
Practice quizzes