High-low point method
High-low point method is a technique used to divide a mixed cost into its variable and fixed components.
Sometimes it is necessary to determine the fixed and variable components of a mixed cost figure. Several techniques are used for this purpose such as scatter graph method, least squares regression method and high-low point method. On this page, we will explain the use of high-low point method.
Under high-low point method, an estimated variable cost rate is calculated using the highest and lowest activity levels and mixed costs figures associated with them. This estimated variable cost rate is used to calculate total estimated variable cost included in the mixed cost figures at highest and lowest activity levels. The estimated variable cost is then subtracted from the total mixed cost figures at highest and lowest activity levels to find the fixed cost component.
The cost function
Like scatter graph method and least squares regression method, high-low point method follows the following cost function (also known as cost volume formula):
Y = a + bX
Where,
- Y = total cost
- a = total fixed cost
- b = fixed cost
- X = number of units
To make the procedure simple and easy to understand, we can divide the calculations into the following three steps.
Steps involved in high-low point method
Step 1 – calculation of variable cost rate:
The first step in high-low point method is to calculate an estimated variable cost rate. This rate is calculated by using the following formula:

Step 2 – calculation of variable cost component:
After calculating estimated variable cost rate, the second step is to calculate the total estimated variable cost at highest and lowest activity levels. It is calculated by multiplying the estimated variable cost rate (calculated in step 1) by highest and lowest activity levels. The formula is given below:
Estimated total variable cost = Estimated variable cost rate × Highest or lowest level of activity
Step 3 – calculation of fixed cost component:
The third and final step in high-low point method is to find out the fixed cost component of the total mixed cost. It is calculated by subtracting the estimated variable cost (calculated in step 2) from the total mixed cost figure. The formula for this purpose is given below:
Fixed cost = Total mixed cost – Estimated total variable
Examples of high-low point method
Let’s take a couple of examples to further elaborate the concept discussed so far.
Example 1:
The Western Company presents the production and cost data for the first six months of the 2015.
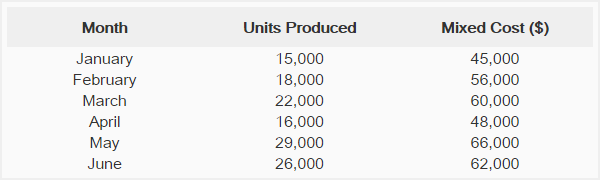
Required: Determine the estimated variable cost rate and fixed cost using high-low point method. Also determine the cost function on the basis of data given above.
Solution:
Variable cost rate:
(66,000 – 45,000)/(29,000 – 15,000)
= $21000/14,000
= $1.5 per unit
Variable cost:
- Highest activity level (May): 29,000 units × $1.5 = $43,500
- Lowest activity level (January): 15,000 × $1.5 = $22,500
Fixed cost:
- Highest activity level (May): $66,000 – $43,500 = $22,500
- Lowest activity level (January): $45,000 – $22,500 = $22,500
On the basis of data provided by Western Company, the cost function is:
Y = $22,500 + $1.5X
Example 2:
Hussain Transport Company operates a fleet of trucks in Michigan. The company has
found that if a delivery truck is driven for 52,500 miles in a month, its average operating cost comes to
45.6 cents per mile. If the same truck is driven for only 35,000 miles in a month, its average
operating cost increases to 53.6 cents per mile.
Required:
- Calculate the estimated variable and fixed cost components of the monthly cost of operating a truck by applying the high-low point method.
- Express the two types of costs in the form of: Y = a + bX.
- If the truck were driven for 40,000 miles during a month, what total cost would the company expect to be incurred?
Solution:
1. Variable and fixed cost components:
Variable cost per mile:
(Cost at high activity – Cost at low activity)/(High activity – Low activity)
= ($23,940* – $18,760**)/(52,500 miles – 35,000 miles)
= $5,180/17,500 miles
= $0.296 per mile
*52,500 x $0.456
**35,000 x $0.536
Fixed cost per month:
Total cost at 52,500 miles – Variable portion
= $23,940 -(52,500 miles x $0.296)
= $23,940 – $15,540
= $8,400
2. Expression:
Y = $8,400 + $0.296X
3. Total cost at 40,000 miles:
Fixed cost + variable cost
= $8,400 + (40,000 miles x $0.296)
= $8,400 + $11,840
= $20,240
Limitations of high-low point method
As compared to scatter graph and least squares regression method, working with high-low point method is simple and easy. However, this method has some serious limitations which the managers must be fully aware of before using it to separate variable and fixed portions of a mixed cost.
The high-low point method uses only two data points (i.e., the highest and the lowest activity levels) which are generally not enough to get the satisfactory results. Moreover, these highest and lowest points often do not represent the usual activity levels of a business entity. The high-low point formula may, therefore, misrepresent the firm’s true cost behavior when it operates at normal activity level.
On account of these defects, high-low point method is considered less accurate when compared with least squares regression method which takes into account all data points and provides much more accurate results.

The solution to example 2 is a bit complicated.
What relationship exit between miles driven and $?
The exchange rate was not given on the question, or is 100 cent = 1$?
Even if it yes, it should have been mention or noted in the question and it should have also been notd that let the question be solved in $ and not cent.
All the determination of cost at high and low activity is not well explained.
Please I request for more elaboration or a similar example which can help me gain more Understanding.