Net present value (NPV) method
Net present value (NPV) method (also known as discounted cash flow method) is a popular capital budgeting technique that takes into account the time value of money. It uses net present value of the investment project as the base to accept or reject a proposed investment in projects like purchase of new equipment, purchase of inventory, expansion or addition of existing plant assets and the installation of new production plants etc.
On this page, first we would explain what is net present value and then look into how it is used to analyze investment projects in capital budgeting decisions.
What is net present value (NPV)?
Net present value is the difference between present value of cash inflows and present value of cash outflows that occur as a result of undertaking an investment project. It may be positive, zero or negative. These three possibilities of NPV metric are briefly explained below:
1. Positive NPV:
If present value of cash inflows is greater than the present value of the cash outflows, the net present value is said to be positive and the investment proposal is considered to be acceptable.
2. Zero NPV:
If present value of cash inflow is equal to present value of cash outflow, the net present value is said to be zero and the investment proposal is considered to be acceptable.
3. Negative NPV:
If present value of cash inflow is less than present value of cash outflow, the net present value is said to be negative and the investment proposal is rejected.
A summary of the NPV concept explained so far is given below:

Let’s take a few examples to illustrate how the net present value method is employed to analyze investment proposals.
Example 1 – cash inflow project
The management of Fine Electronics Company is considering to purchase an equipment to be attached with the main manufacturing machine. The equipment will cost $6,000 and will increase annual cash inflow by $2,200. The useful life of the equipment is 6 years. After 6 years it will have no salvage value. The management wants a 20% return on all investments.
Required:
- Compute net present value (NPV) of this investment project.
- Should the equipment be purchased according to NPV analysis?
Solution:
(1) Computation of net present value:

*Value from “present value of an annuity of $1 in arrears table“.
(2) Purchase decision:
Yes, the equipment should be purchased because the net present value is positive ($1,317). Having a positive net present value means the project promises a rate of return that is higher than the minimum rate of return required by management (20% in the above example).
In the above example, the minimum required rate of return is 20%. It means if the equipment is not purchased and the money is invested elsewhere, the company would be able to earn 20% return on its investment. The minimum required rate of return (20% in our example) is used to discount the cash inflow to its present value and is, therefore, also known as discount rate.
Investments in assets are usually made with the intention to generate revenue or reduce costs in future. The reduction in cost is considered equivalent to increase in revenues and should, therefore, be treated as cash inflow in capital budgeting computations.
The net present value method is used not only to evaluate investment projects that generate cash inflow but also to evaluate projects that can reduce costs. The following example illustrates how this capital budgeting method can be applied to analyze a cost reduction project:
Example 2 – cost saving project
Smart Manufacturing Company is planning to reduce its labor costs by automating a critical task that is currently performed manually. The automation requires the installation of a new machine which would cost $15,000 to purchase and install. This new machine can reduce annual labor cost by $4,200 and has a useful life of approximately 15 years. The salvage value of the machine after fifteen years will be zero. The required rate of return of Smart Manufacturing Company is 25%.
Should Smart Manufacturing Company purchase the new machine if evaluated using an NPV method?
Solution:
According to net present value method, Smart Manufacturing Company should purchase the machine because the present value of the cost savings is greater than the present value of the initial cost to purchase and install the machine. The computations are given below:

*Value from “present value of an annuity of $1 in arrears table“.
Net present value (NPV) method with uneven cash flow
Notice that the projects in above two examples generate equal cash inflow in all the periods (the cost saving in example 2 has been treated as cash inflow). Such cash flow is known as even cash flow. However, projects often do not generate equal cash inflows in all the periods. When projects generate different cash inflows in different periods, the flow of cash is known as uneven cash flow. To analyze such projects, the present value of cash inflows is determined for each period separately. It has been illustrated by example 3 below:
Example 3 – uneven cash flows
A project requires an initial investment of $225,000 and is expected to generate the following net cash inflows over its four years life:
Year 1: $95,000
Year 2: $80,000
Year 3: $60,000
Year 4: $55,000
Required: Compute net present value of the project if the minimum desired rate of return is 12%.
Solution:
The cash inflow generated by the project is uneven. Therefore, the present value would be computed for each year separately:
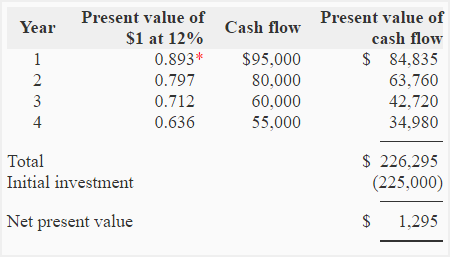
*Value from “present value of $1 table“.
The project seems attractive because its net present value (NPV) is positive.
Choosing among several alternative proposals
Many times, a company may have limited funds but several alternative proposals. In such circumstances, if each alternative requires the same amount of investment, the one with the highest net present value is preferred. However, if each proposal requires a different amount of investment, then the above procedure of project evaluation would not work. In such circumstances, proposals are ranked by computing an index called profitability index (sometimes referred to as present value index). The proposal with the highest profitability index is considered the best for investment. Profitability index is computed using the following formula:
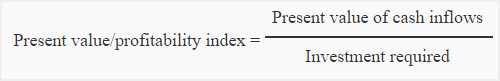
Example 4 – choosing among several alternative projects
Choose the most desirable investment proposal from the following alternatives using profitability index method:

Solution:
Because each investment proposal requires a different amount of investment, the most desirable investment can be found using present value index. Present value index of all three proposals is computed below:
Proposal X: 212,000/200,000 = 1.06
Proposal Y: 171,800/160,000 = 1.07
Proposal Z: 185,200/180,000 = 1.03
Proposal X has the highest net present value but is not the most desirable investment. The present value indexes show proposal Y as the most desirable investment because it promises to generate 1.07 present value for each dollar invested, which is the highest among three alternatives.
Underlying assumptions of NPV approach
The net present value method of project analysis is based on two prime assumptions which are given below:
- The cash generated by a project is immediately reinvested to generate a return at a rate that is equal to the discount rate used in present value analysis.
- The inflows and outflows of cash other than initial investment occur at the end of the period.
Advantages and disadvantages NPV method
The basic advantage of net present value method is that it considers the time value of money while evaluating the proposals’ viability. The disadvantage of NPV approach is that it is more complex than other methods that do not consider present value of cash flows. Furthermore, it assumes immediate reinvestment of the cash generated by projects being analyzed. This assumption might not always be appropriate due to changing economic conditions.

Leave a comment