Exercise-27: Net present value (NPV) analysis – total and incremental cost approach

Learning objective:
While comparing competing proposals under net present value (NPV) method, we can follow either the total or the incremental cost approach. This problem illustrates the use of both the approaches in an NPV analysis.

National Transport Company has a number of large trucks. One of the trucks is in poor condition and needs an immediate renovation at a cost of $100,000. An overhaul of engine will also be needed 6-years from now at a cost of $10,000. If these costs are incurred, the truck will be useful for 12 years. After 12-year period, it will be sold at a salvage value (scrap value) of $30,000. At this time, the salvage value of the truck is $35,000. The total annual revenues of the truck will be $200,000 and the total cost to operate the truck will be $150,000 per year.

Alternatively, National Transport Company can purchase a new truck for $180,000. The new truck will require some repairs at the end of 6-year period at a cost of $5,000. Its salvage value will be $30,000 after its useful life of 12 years. The total annual revenues of the new truck will be $200,000 and its operating cost will be $110,000 per year.

The company’s required rate of return is 15% before taxes.

Required: Should National Transport Company renovate the old truck or purchase a new truck. Use the following approaches to net present value (NPV) analysis for your answer:

1. Total cost approach.
2. Incremental cost approach.

(Ignore income tax in your computations.)

 Solution:

(1) Total cost approach to NPV:

In total cost approach, net present values of all alternative proposals are computed separately using all the inflows and outflows of cash involved. Since the NPV for each proposal is calculated independent of each other, the method can be applied even if more than two projects are being compared. This is a distinct advantage of total cost approach. Let’s select the best of two proposals using this approach:

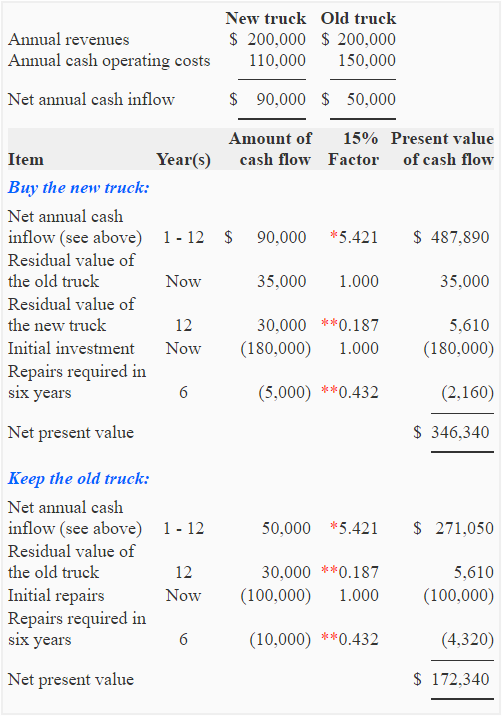
* Value from “present value of an annuity of $1 in arrears table“.
**Value from “present value of $1 table”.

Net present value in favor of buying the new truck:

NPV with new truck – NPV with old truck
= $346,340 – $172,340
= $174,000

Since the NPV of new truck surpasses the NPV of old truck by $174,000, the company should buy the new truck rather than renovating the old one.

(2) Incremental cost approach to NPV:

Unlike the method used in above solution, incremental cost approach focuses only on those cash flows (both inflows and outflows) that differ between the proposals being considered. This method works in situations where only two projects are under consideration. Let’s solve the question using incremental cost method:

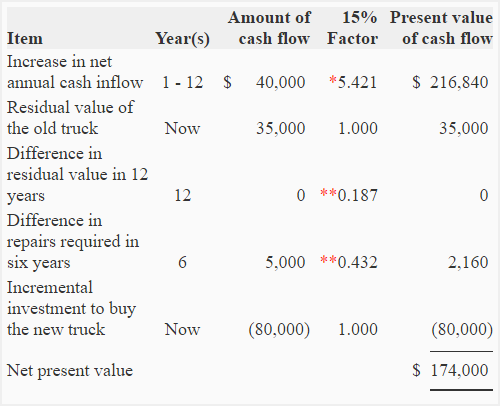
* Value from “present value of an annuity of $1 in arrears table“.
**Value from “present value of $1 table“.