Exercise-1: Simultaneous equations method of cost distribution

The cost data relating to two service departments and two production departments of Good Master Company for the month of March, 2018 is given below:

Production departments costs:

Department K: $25,000
Department L: $20,000

Service departments costs:

Department M: $5,000
Department N: $4,400

The percentages by which the costs of service department M and N are to be distributed are as follows:

Department M:
50% to department K, 40% to department L and 10% to department N

Department N:
40% to department K, 40% to department L and 20% to department M

Required: Distribute the service departments costs using simultaneous equations method.

Solution

Under simultaneous equations method, the costs of service departments are distributed to each other as well as to production departments. This method requires the use of simultaneous equations.

The cost of service department M after receiving the share from service department N:

M = $5,000 + 0.2N —— Equation 1

The cost of service department N after receiving the share from service department M:

N = $4,400 + 0.1M —— Equation 2

By putting the value of N in equation 1:

M = $5,000 + 0.2N
M = $5,000 + 0.2($4,400 + 0.1M)
M = $5,000 + $880 + 0.02M
M – 0.02M = $5,880
0.98M = $5,880
M = $5,880/0.98
M = $6,000

By putting the value of M in equation 2:

N = $4,400 + 0.1M
N = $4,400 + 0.1($6,000)
N = $4,400 + $600
N = $5,000

Cost distribution summary

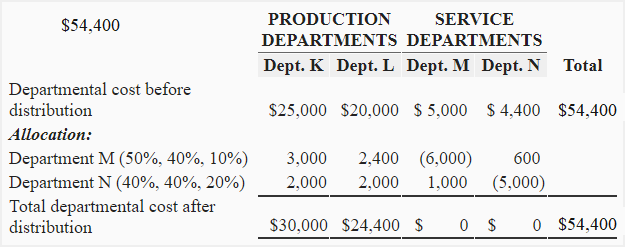
Supporting computations:

Distribution of department M cost:

• Distributed to department K: $6,000 × 0.5 = $3,000
• Distributed to department L: $6,000 × 0.4 = $2,400
• Distributed to department N: $6,000 × 0.1 = $600

Distribution of department N cost:

• Distributed to department K: $5,000 × 0.4 = $2,000
• Distributed to department L: $5,000 × 0.4 = $2,000
• Distributed to department M: $5,000 × 0.2 = $1,000