Economic order quantity (EOQ)

Definition and explanation

Economic order quantity (EOQ) is the order size that minimizes the sum of ordering and holding costs related to raw materials or merchandise inventories. In other words, it is the optimal inventory size that should be ordered with the supplier to minimize the total annual inventory cost of the business. Other names used for economic order quantity are optimal order size and optimal order quantity.

The economic order quantity is computed by both manufacturing companies and merchandising companies. Manufacturing companies compute it to find the optimal order size of raw materials inventory and merchandising companies compute it to find the optimal order size of ready to use merchandise inventory.

The ordering and holding costs

The two significant factors that are considered while determining the economic order quantity (EOQ) for any business are the ordering costs and the holding costs. A brief explanation of both the costs is given below:

Ordering costs

The ordering costs are the costs that are incurred every time an order for inventory is placed with the supplier. Examples of these costs include telephone charges, delivery charges, invoice verification expenses and payment processing expenses etc. The total ordering cost usually varies according to the frequency of placing orders. Mostly, it is directly proportional to the number of orders placed during the year which means If the number of orders placed during the year increases, the annual ordering cost will also increase and if, on the other hand, the number of orders placed during the year decreases, the annual ordering cost will also decrease.

Holding costs

The holding costs (also known as carrying costs) are the costs that are incurred to hold the inventory in a store or warehouse. Examples of costs associated with holding of inventory include occupancy of storage space, rent, shrinkage, deterioration, obsolescence, insurance and property tax etc. The total holding cost usually depends upon the size of the order placed for inventory. Mostly, the larger the order size, the higher the annual holding cost and vice versa. The total holding cost is some time expressed as a percentage of total investment in inventory.

The economic order quantity is the level of quantity at which the combined ordering and holding cost is at the minimum level.

Relation between the ordering and holding cost:

There is an inverse relationship between ordering cost and holding cost. Keeping the annual demand constant if for example the number of orders decreases, the ordering cost will also decrease but the holding cost will rise and vice versa.

Economic order quantity formula

The following formula is used to determine the economic order quantity (EOQ):

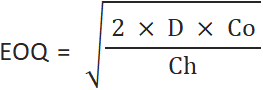
Where,

• D = Demand per year, generally referred to as annual demand
• Co = Cost per order, generally referred to as ordering cost
• Ch = Cost of holding per unit of inventory, generally referred to as holding cost

Examples

Example 1

The material DX is used uniformly throughout the year. The data about annual requirement, ordering cost and holding cost of this material is given below:

• Annual requirement: 2,400 units
• Ordering cost: $10 per order
• Holding cost: $0.30 per unit

Required: Determine the economic order quantity (EOQ) of material DX using above data.

Solution

EOQ calculation:

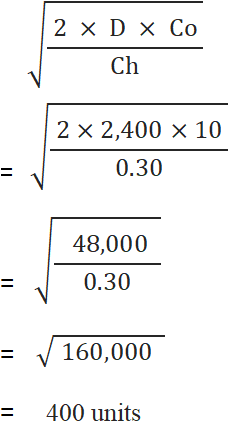
The economic order quantity for material DX is 400 units. Now, we can compute the number of orders to be placed per year, annual ordering cost, annual holding cost and combined annual ordering and holding cost as follows:

Number of orders per year

= Annual demand/EOQ
= 2,400 units/400 units
= 6 orders per year

Ordering cost

= Number or orders per year × Cost per order
= 6 orders × $10
= $60

Holding cost

= Average units × Holding cost per unit
= (400/2) × 0.3
= $60

Combined ordering and holding cost at economic order quantity (EOQ):

= Ordering cost + Holding cost
= $60 + $60
= $120

Notice that both ordering cost and holding cost are $60 at economic order quantity. The holding cost and ordering cost at EOQ tend to be the same.

Example 2

The John Sports Inc. purchases tennis balls at $20 per dozen from its suppliers. The John Sports will sell 34,300 dozen of tennis balls evenly throughout the year. The total cost to handle a purchase order is $10. The insurance, property tax and rent for each dozen tennis balls in the average inventory is $0.40. The company wants a 5% return on average inventory investment.

Required:

1. Compute the economic order quantity.
2. Compute the total annual inventory expenses to sell 34,300 dozen of tennis balls if orders are placed according to economic order quantity computed in part 1.

Solution

1. Economic order quantity:

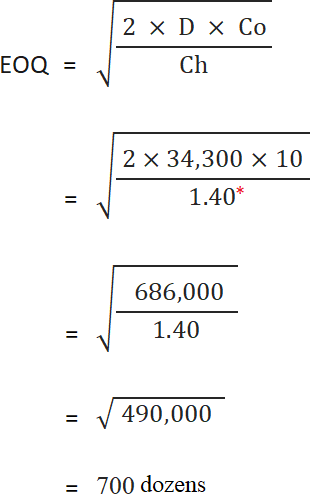
*$0.40 + ($20 × 5/100) = $1.40

2. Total annual inventory expenses to sell 34,300 dozen of tennis balls:

= Annual ordering cost + Annual holding cost
= (Number of orders × Cost per order) + (Average units × Holding cost per unit)
= (*49 orders × $10) + [(700/2) × 1.4]
= $490 + $490
= $980

*Number of orders to be placed: 34,300/700 = 49 orders

Tabular determination of economic order quantity (EOQ)

Under tabular approach of determining economic order quantity, the combined ordering and holding cost is computed at different number of orders and their respective order quantities. This approach is also known as trial-and-error approach of determining economic order quantity.

This approach is illustrated below using the same data as used in the example 1 given above:

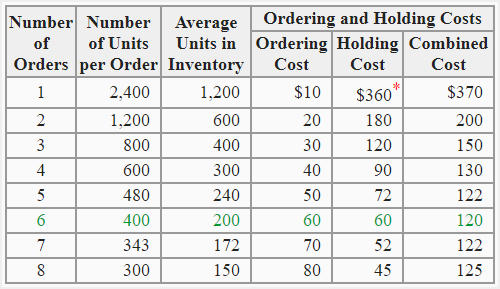
*Average units × Holding cost per unit: 1,200 units × 0.30 = $360

Notice that the quantity of 400 units with 6 annual orders and a combined ordering and holding cost of $120 is the most economical quantity to order. Other order quantities that result in more or less than six orders per year are not so economical. For example, if only one order for the whole annual requirement of 2,400 units is placed, the combined ordering and holding cost comes to $370 which is far higher than the cost at economic order quantity of 400 units.

The application of tabular approach is not common as it is more time consuming as compared to formula approach. Moreover, in some situations, it provides only an estimate of economic order quantity and is therefore not as accurate as the formula approach. If a question regarding economic order quantity is asked in the examination, the students should avoid using tabular (trial and error) approach; rather they should use the formula approach which is comparatively less time consuming and which also provides the most accurate answer.

Underlying assumptions of economic order quantity (EOQ)

The computation of economic order quantity (EOQ) is based on the following assumptions:

1. The total number of units to be consumed during the period is known with certainty.
2. The total ordering cost remains constant throughout the period.
3. The inventory cost remains constant throughout the period.
4. There are no cash or quantity discounts available.
5.  The whole quantity of ordered inventory is delivered in one batch.
6. The optimal quantity for each invariable or stock item is computed separately.
7. The lead time does not fluctuate and the order is received on time with the total order quantity.

The assumptions described above are also known as the limitations of economic order quantity (EOQ).